Definition

A dendrogram is a network structure. It is constituted of a root node that gives birth to several nodes connected by edges or branches. The last nodes of the hierarchy are called leaves. In the following example, the CEO is the root node. He manages 2 managers that manage 8 employees (the leaves).

# libraries
library(ggraph)
library(igraph)
library(tidyverse)
library(dendextend)
library(colormap)
library(kableExtra)
options(knitr.table.format = "html")

# create a data frame 
data=data.frame(
  level1="CEO",
  level2=c( rep("boss1",4), rep("boss2",4)),
  level3=paste0("mister_", letters[1:8])
)
 
# transform it to a edge list!
edges_level1_2 = data %>% select(level1, level2) %>% unique %>% rename(from=level1, to=level2)
edges_level2_3 = data %>% select(level2, level3) %>% unique %>% rename(from=level2, to=level3)
edge_list=rbind(edges_level1_2, edges_level2_3)
 
# Now we can plot that
mygraph <- graph_from_data_frame( edge_list )
ggraph(mygraph, layout = 'dendrogram', circular = FALSE) + 
  geom_edge_diagonal() +
  geom_node_point(color="#69b3a2", size=3) +
  geom_node_text(
    aes(  label=c("CEO", "Manager", "Manager", LETTERS[8:1]) ), 
    hjust=c(1,0.5, 0.5, rep(0,8)), 
    nudge_y = c(-.02, 0, 0, rep(.02,8)),
    nudge_x = c(0, .3, .3, rep(0,8))
  ) +
  theme_void() +
  coord_flip() +
  scale_y_reverse()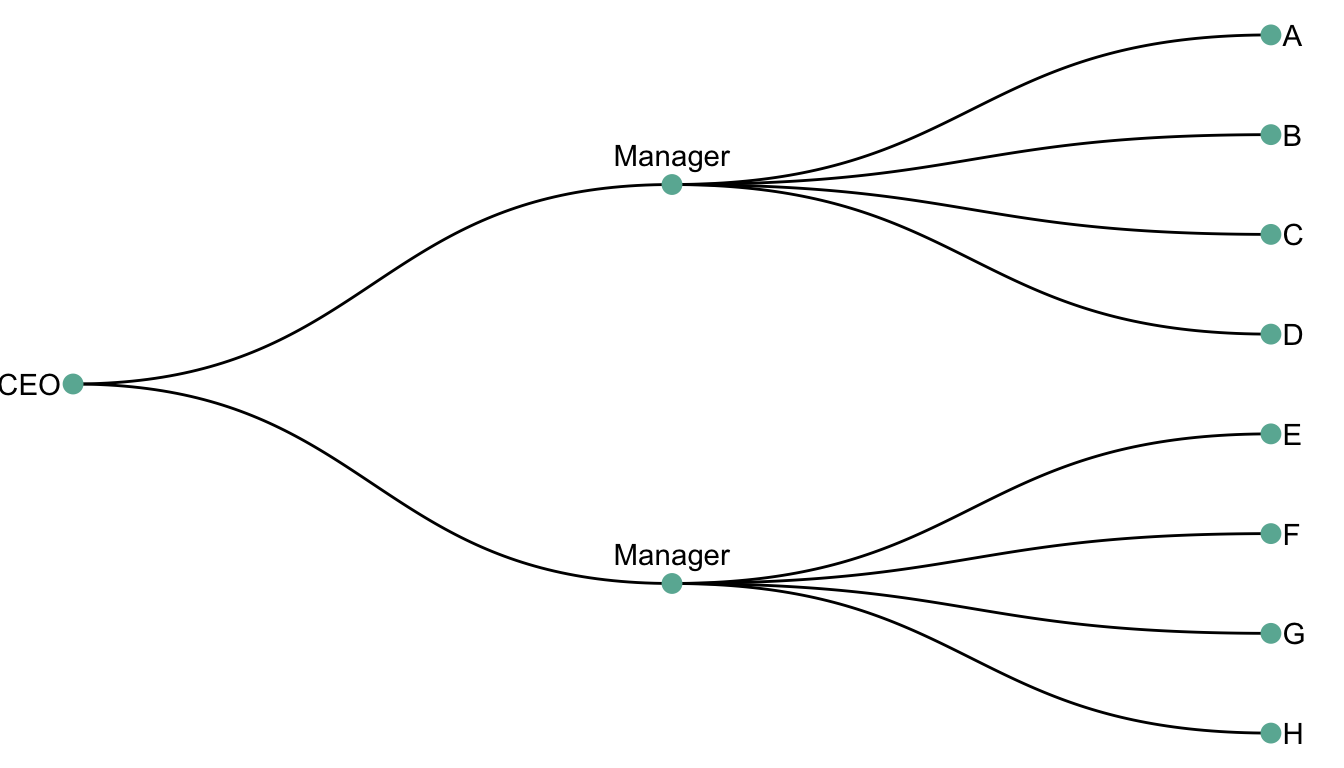

Two type of dendrogram exist, resulting from 2 types of dataset:

A hierarchic dataset provides the links between nodes explicitely. Like above.
The result of a clustering algorythm can be visualized as a dendrogram.

Dendrogram from hierarchic data

Dendrogram from clustering

Let’s consider a distance matrix that provides the distance between all pairs of 28 major cities. Note that this kind of matrix can be computed from a multivariate dataset, computing distance between each pair of individual using correlation or euclidean distance.

# Load the data
data <- read.table("https://raw.githubusercontent.com/holtzy/data_to_viz/master/Example_dataset/13_AdjacencyUndirecterWeighted.csv", header=T, row.names="Cities.", sep=",") %>% as.matrix
colnames(data) <- gsub("\\.", " ", colnames(data))

# show data
tmp <- data %>% as.data.frame() %>% select(1,3,6) %>% .[c(1,3,6),]
tmp[is.na(tmp)] <- "-"
tmp %>% kable() %>%
  kable_styling(bootstrap_options = "striped", full_width = F)

	Berlin	Cairo	Caracas
Berlin		1795	5247
Cairo	1795		6338
Caracas	5247	6338

It is possible to perform hierarchical cluster analysis on this set of dissimilarities. Basically, this statistical method seeks to build a hierarchy of clusters: it tries to group sample that are close one from another.

The result can be seen as a dendrogram:

# Perform hierarchical cluster analysis.
dend <- as.dist(data) %>% 
  hclust(method="ward.D") %>% 
  as.dendrogram()

# Plot with Color in function of the cluster
leafcolor <- colormap(colormap = colormaps$viridis, nshades = 5, format = "hex", alpha = 1, reverse = FALSE)
par(mar=c(1,1,1,7))
dend %>%
  set("labels_col", value = leafcolor, k=5) %>%
  set("branches_k_color", value = leafcolor, k = 5) %>%
  plot(horiz=TRUE, axes=FALSE)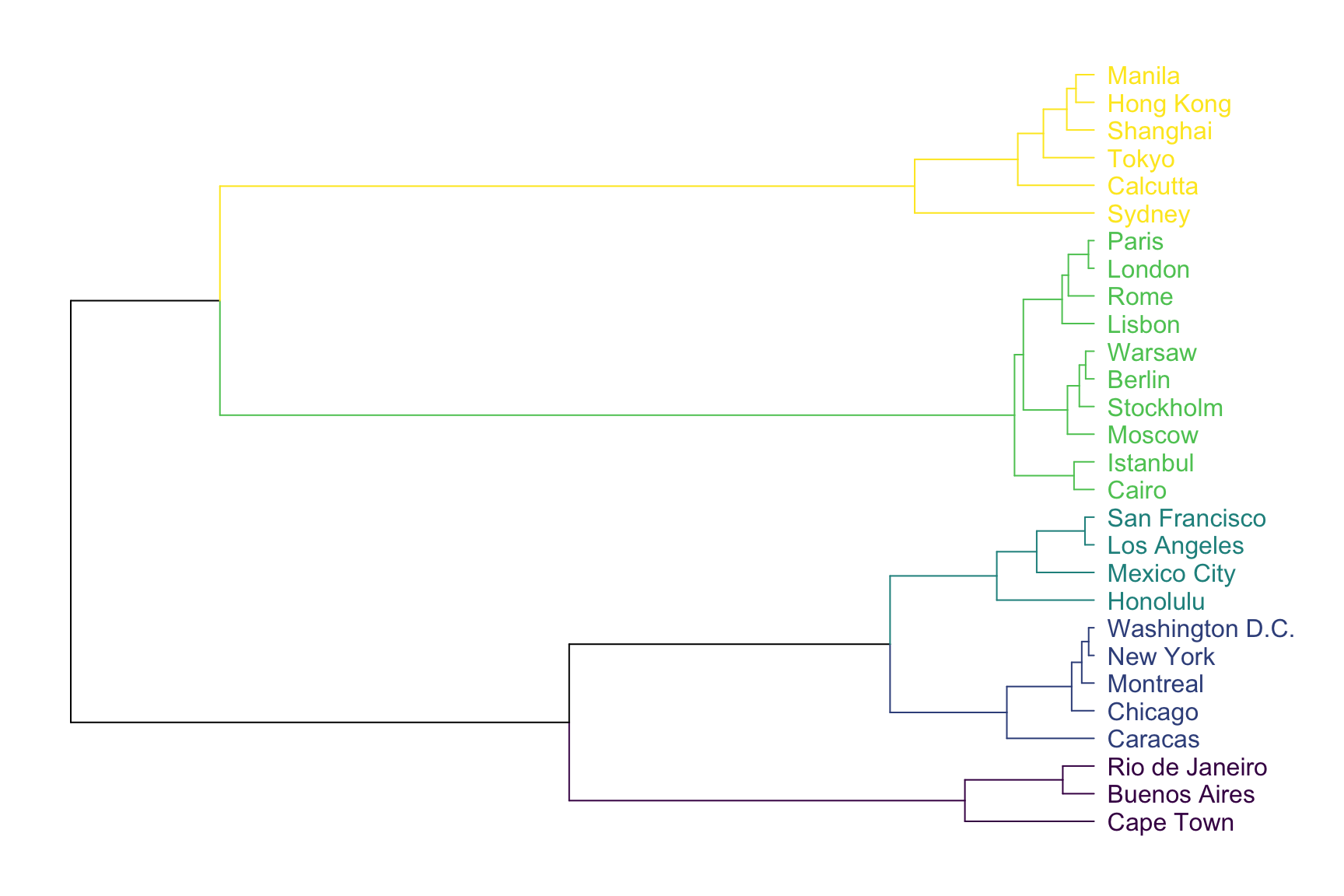

As expected, cities that are in same geographic area tend to be clusterized together. For example, the yellow cluster is composed by all the Asian cities of the dataset. Note that the dendrogram provides even more information. For instance, Sydney appears to be a bit further to Calcutta than calcutta is from Tokyo: this can be deduce from the branch size that represents the distance.

A common task consists to compare the result of a clustering with an expected result. For instance, we can check if the countries are indeed grouped in continent using a color bar:

# Create a color vector with continent
continent <- c("Europe", "South America", "Africa", "Asia", "Africa", "South America", "North America", "Asia", "North America", 
               "Europe", "Europe","Europe", "North America", "Asia", "South America", "North America", "Europe", "North America",
               "Europe", "South America", "Europe", "North America", "Asia", "Europe", "Asia", "Asia", "Europe",
               "North America"
               )
barcolor <- colormap(colormap = colormaps$viridis, nshades = 5, format = "hex", alpha = 1, reverse = FALSE)
barcolor <- barcolor[as.numeric(as.factor(continent))]

# Make the dendrogram
par(mar=c(10,2,2,2))
dend %>%
  set("labels_col", value = leafcolor, k=5) %>%
  set("branches_k_color", value = leafcolor, k = 5)  %>%
  plot(axes=FALSE)

colored_bars(colors = barcolor, dend = dend, rowLabels = "continent")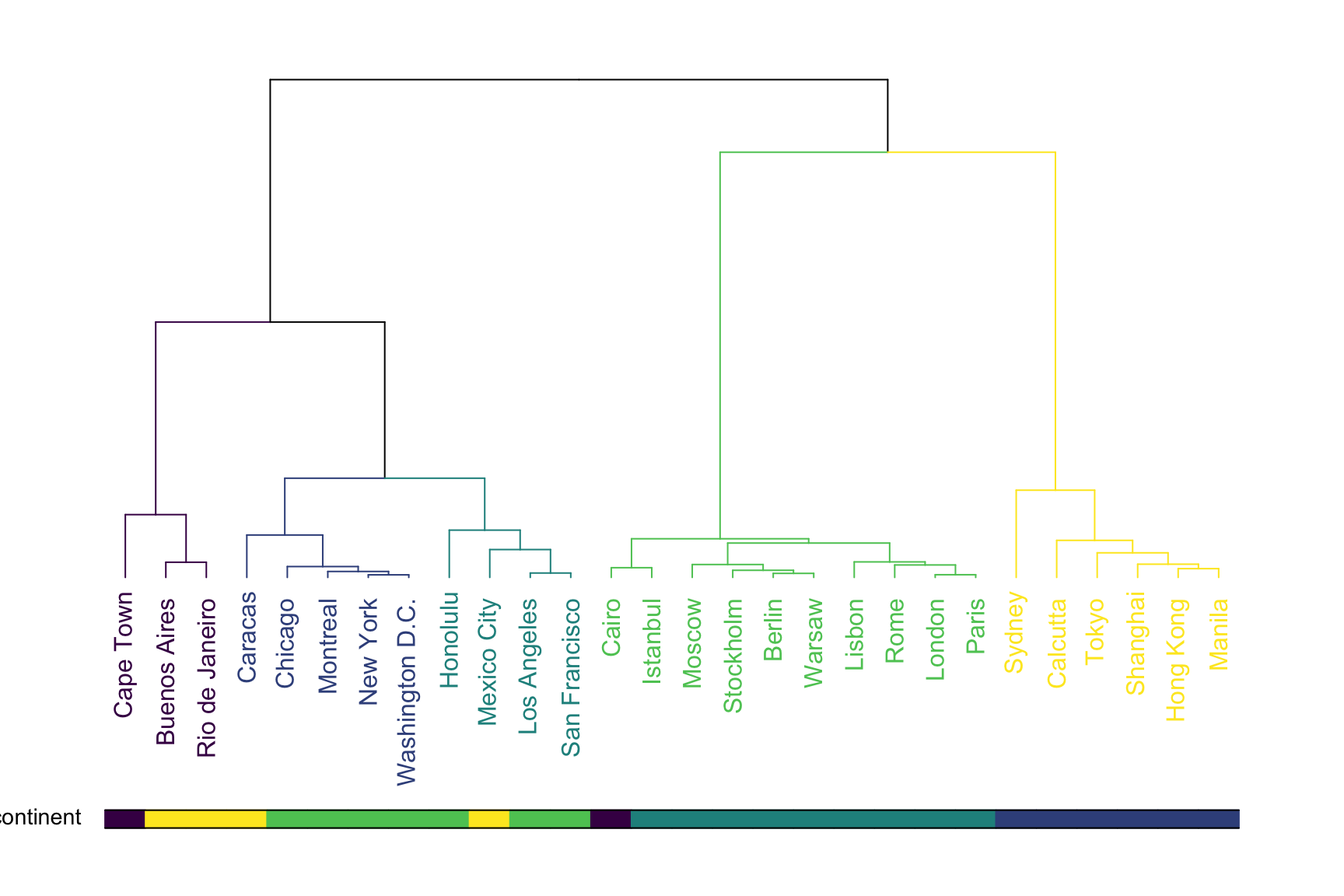

This graphic allows to validate that the clustering indeed grouped cities by continent. There are a few discrepencies that are logical. Indeed, Mexico city has been considered as a city of South America here, altough it is probably closer from North America as suggested by the clustering.

Variation

Many variations exist for dendrogram. It can be horizontal or vertical as shown before. It can also be linear or circular. The advantage of the circular verion being that it uses the graphic space more efficiently:

# Libraries
library(ggraph)
library(igraph)
library(tidyverse)
library(RColorBrewer) 
set.seed(1)

# create a data frame giving the hierarchical structure of your individuals
d1=data.frame(from="origin", to=paste("group", seq(1,10), sep=""))
d2=data.frame(from=rep(d1$to, each=10), to=paste("group", seq(1,100), sep="_"))
edges=rbind(d1, d2)
 
# create a vertices data.frame. One line per object of our hierarchy
vertices = data.frame(
  name = unique(c(as.character(edges$from), as.character(edges$to))) , 
  value = runif(111)
) 
# Let's add a column with the group of each name. It will be useful later to color points
vertices$group = edges$from[ match( vertices$name, edges$to ) ]
 
 
#Let's add information concerning the label we are going to add: angle, horizontal adjustement and potential flip
#calculate the ANGLE of the labels
vertices$id=NA
myleaves=which(is.na( match(vertices$name, edges$from) ))
nleaves=length(myleaves)
vertices$id[ myleaves ] = seq(1:nleaves)
vertices$angle= 90 - 360 * vertices$id / nleaves
 
# calculate the alignment of labels: right or left
# If I am on the left part of the plot, my labels have currently an angle < -90
vertices$hjust<-ifelse( vertices$angle < -90, 1, 0)
 
# flip angle BY to make them readable
vertices$angle<-ifelse(vertices$angle < -90, vertices$angle+180, vertices$angle)
 
# Create a graph object
mygraph <- graph_from_data_frame( edges, vertices=vertices )

# prepare color
mycolor <- colormap(colormap = colormaps$viridis, nshades = 6, format = "hex", alpha = 1, reverse = FALSE)[sample(c(1:6), 10, replace=TRUE)]

# Make the plot
ggraph(mygraph, layout = 'dendrogram', circular = TRUE) + 
  geom_edge_diagonal(colour="grey") +
  scale_edge_colour_distiller(palette = "RdPu") +
  geom_node_text(aes(x = x*1.15, y=y*1.15, filter = leaf, label=name, angle = angle, hjust=hjust, colour=group), size=2.7, alpha=1) +
  geom_node_point(aes(filter = leaf, x = x*1.07, y=y*1.07, colour=group, size=value, alpha=0.2)) +
  scale_colour_manual(values= mycolor) +
  scale_size_continuous( range = c(0.1,7) ) +
  theme_void() +
  theme(
    legend.position="none",
    plot.margin=unit(c(0,0,0,0),"cm"),
  ) +
  expand_limits(x = c(-1.3, 1.3), y = c(-1.3, 1.3))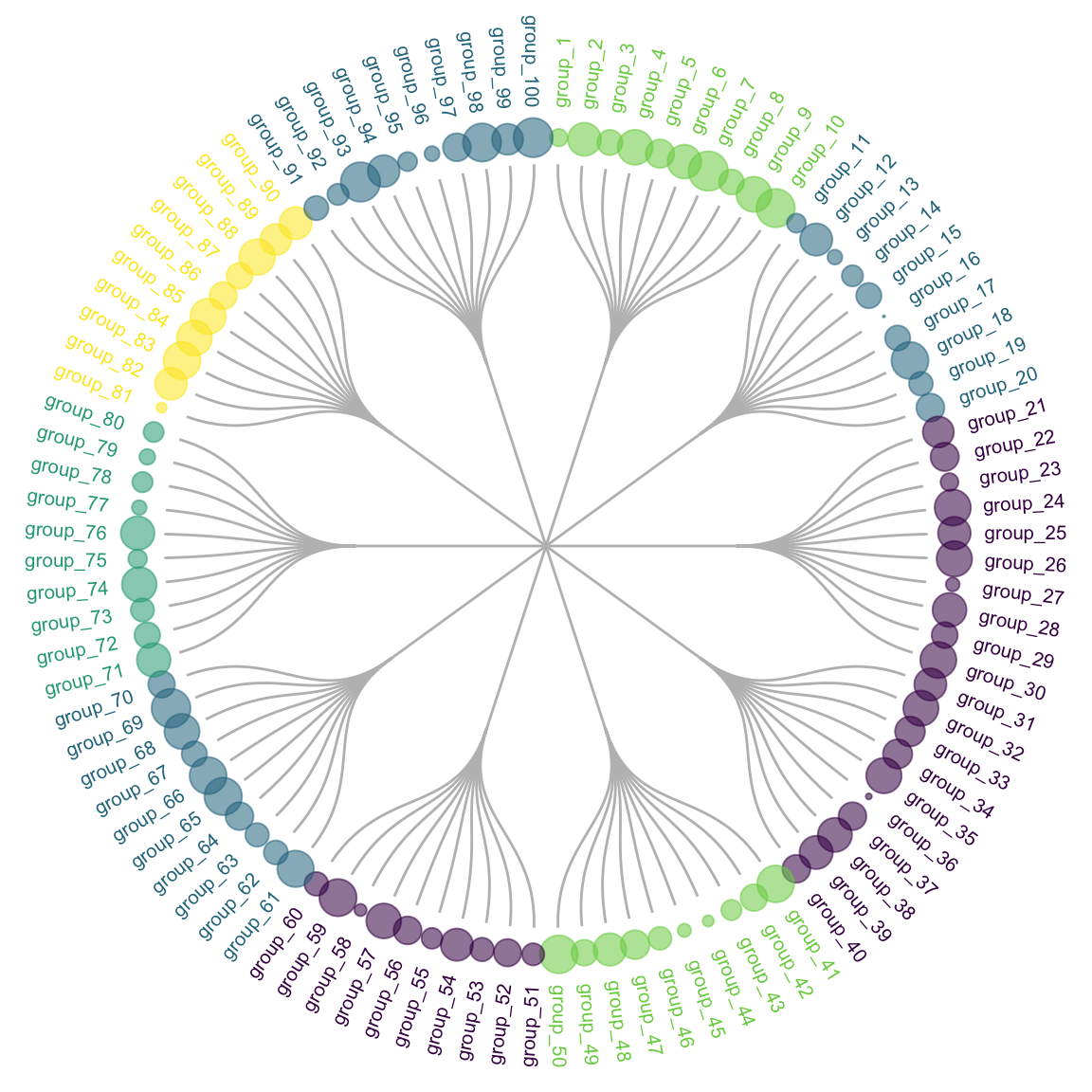

Another common variation is to display a heatmap at the bottom of the dendrogram. Indeed, it allows to visualize the distance between each sample and thus to understand why the clustering algorythm put 2 samples next to each other.

library(d3heatmap)
d3heatmap(mtcars, scale = "column", colors = "Blues")

Common mistakes

If using a clustering algorythm, be sure you understood which metrics have been used for the distance calculation and for the clustering algorythm.
Horizontal version are appreciated with long labels
Showing the heatmap is a good practice if you’re working with clustering.

Build your own

The R and Python graph galleries are 2 websites providing hundreds of chart example, always providing the reproducible code. Click the button below to see how to build the chart you need with your favorite programing language.

R graph gallery

Comments

Any thoughts on this? Found any mistake? Disagree? Please drop me a word on twitter or in the comment section below: